対称性　―図形、多項式、時空間―

　対称性をもつということは、ある変換の下での不変量を持つことだ。例えば、ある関数$f(x)$があって、これに対して変数変換 $x→x’$を考える。一般的に変数変換の結果 $ f(x) →f'(x’)$となり、関数形自体が変わってしまうだろう。しかし、特別な状況 $f(x)= f(x’) $となる場合を対称性を持つと表現するのだ。数学や物理でどのような対称性があるのか簡単にまとめた。

図形の対称性
多項式の対称性
時空間の対称性
ゲージ対称性
参考

図形の対称性

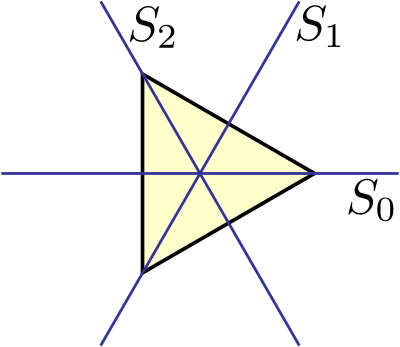
　最もわかりやすいのは図形の対称性だ。例えば正三角形の対称性について考える。どのような変換が正三角形を不変に保つだろうか。図形の中心を回転軸とした0°、120°、240°回転 $R_{1},R_{2},R_{3}$ は正三角形を不変に保つ。また、3つの軸に関する鏡映$S_{1},S_{2},S_{3}$も不変に保つ。このような図形を不変に保つ対称操作全体の集合
$$D_3=\{R_{1},R_{2},R_{3}, S_{1},S_{2},S_{3} \}$$
は群を成すことを確かめることができる。この群は二面体群$D_3$と呼ばれる。正三角形の頂点に番号を振るとこれらの番号の置換を行うことと同じであるから対称群$S_3$と群同型でもある。
$$D_3\cong\:S_3$$

多項式の対称性

　代数的な対象である多項式に対しても対称性を考えることができる。例えば、$$x^2+xy+y^2$$について考えると$x$と$y$の入れ替えについて不変であるから対称式と呼ばれる。文字の入れ替えという演算が群を成していることを確かめられる。群には方程式の「形」についての情報が含まれているといえる。
　一般３次方程式$x^3+ax^2+bx+c=0$の解を$\alpha,\beta,\gamma$とする。この時、解と係数の関係から
\begin{eqnarray}
\left\{
\begin{array}{l}
\alpha\:+\beta\:+\gamma=-a\\
\alpha\:\beta\: + \beta\: \gamma+ \gamma\: \alpha =b\\
\alpha\:\beta\:\gamma=-c
\end{array}
\right.
\end{eqnarray}

これらは解に関する対称式であり、解の置換に関して不変だ。この置換が成す群は、方程式のGalois群と呼ばれ、一般３次方程式の場合は $S_3$となっている。正三角形と同じ対称性ということだ。 Galois 群は方程式が代数的に解けるかどうかの判定に関係している。

時空間の対称性

　物質が存在する時空間も対称性を持っている。解析力学では運動方程式が空間並進、空間回転、時間並進の座量変換について対称性を持つことから、それぞれ運動量保存則、角運動量保存則、エネルギー保存則が導かれる。（ Noetherの定理）宇宙に特別な場所は無い、という宇宙原理から保存則が導かれるわけだ。逆に宇宙原理とのずれが見つかれば、保存則が厳密には成り立たないことになるのだろうか？話が逸れたが、特に物質の存在を仮定するわけでもなく、運動方程式が座標変換で形を変えないことから種々の保存則が導かれることから、これら保存則は時空そのものが持つ対称性に由来しているといえる。

ゲージ対称性

　ゲージ対称性という概念は上述の対称性と比べるととらえどころのない感じのする概念だ。どうしてこうのような概念にたどり着くことができたのだろう。数学や理論物理学の世界は一部の天才によるブレークスルーで発展する側面があるので私のような凡人にはなかなか理解しにくいところだ。そして、ゲージ理論を理解しようと思うと微分幾何学などを理解する必要があるため門外漢にはなかなか敷居が高い。
　ゲージ対称性というのはゲージ変換というある種の座標変換の下でのラグランジアンと運動方程式の不変性を指している。同じ運動方程式を与えるラグランジアンは一意ではなく自由度があるということだ。要するにラグランジアンに変更を加えたとしても、作用積分の変分から導かれる運動方程式の形に変化がなければいいのである。作用積分は次式で表される。
$$I=\int L(\boldsymbol{x},\dot{\boldsymbol{x}},t)dt\tag{1}$$
例えば、この式中のラグランジアンに
$$\frac{df}{dt}=\frac{ \partial f }{ \partial t }+\displaystyle \sum_{i=1}^3 \frac{ \partial f }{ \partial x^{i} } \frac{dx^{i}}{dt}\tag{2}$$
という形の式を足して$I’$としても、

$$I’=\int \left[L( \boldsymbol{x},\dot{\boldsymbol{x}},t)+ \frac{df}{dt}\right]dt=I+\int \frac{df}{dt}dt=I+const. \tag{3}$$

と定数の分しか変わらないから、変分としては変化せず、運動方程式の形も変わらない。ここでラグランジアンを

$$L(\boldsymbol{x},\dot{\boldsymbol{x}},t)=T(\dot{\boldsymbol{x}})-V(\boldsymbol{x},\dot{\boldsymbol{x}},t)\tag{4}$$

としたとき、ポテンシャル$V$の形をうまく選べばラグランジアンの形も変えないようにできるのではないだろうか。実際、
　

$$V(\boldsymbol{x},\dot{\boldsymbol{x}},t ) =V_{0}(\boldsymbol{x},t)+ \displaystyle \sum_{i=1}^3 V_{i}(\boldsymbol{x},t)\dot{x}^{i}\tag{5}$$

という形のポテンシャルを考えると、ラグランジアンは

$$V_{0}→ V_{0} – \frac{ \partial f }{ \partial t } , V_{i}→ V_{i} – \frac{ \partial f }{ \partial x^{i} } \tag{6} $$

という変換の下で不変になる。それは$L’=L+\frac{df}{dt}$を計算してみるとわかる。実は、電磁場のポテンシャルは(5)式の形をしている、というよりラグランジアンの形を変えないようなポテンシャルを選ぶと電磁場が出てくるといった方がいいのかもしれない。電磁場のポテンシャルはこうだ。

$$V(\boldsymbol{x},\dot{\boldsymbol{x}},t ) =q\{\phi(\boldsymbol{x},t)- \displaystyle \sum_{i=1}^3 A_{i}(\boldsymbol{x},t)\dot{x}^{i}\}\tag{7}$$

このとき、$f=qu$とすると

$$\phi_{0}→ \phi_{0} – \frac{ \partial u }{ \partial t } , A_{i}→ A_{i} + \frac{ \partial f }{ \partial x^{i} } \tag{8}$$

と変換される。これを大域的ゲージ変換という。
　ゲージ変換にももう一つ種類があって局所的ゲージ変換というものがある。ここでは詳しく述べることは筆者の能力を超えるので行わず、概要を述べるにとどめる。まず、何故そのような局所的な座標変換を考える必要があるのかというと、一般相対性理論（重力の理論）と電磁気学などのその他の物理理論を統合するためだ。一般相対性理論がそれ以前の力学、電磁気学、特殊相対性理論と異なるのは、理論の舞台となる時空間そのものが平らでなく「曲がっている」ところだ。そのため、ガリレイ変換やローレンツ変換のような大域的な変換な成り立たず、局所的な変換を考える必要がある。つまり、ある点の近傍だけ考えれば平らな時空間とみなせるので、ある点の周りでのみ成立する対称性を考えるということだ。そのうち書けるようになれば記事にまとめようと思う。

参考

橋本義武. ゲージ理論の基礎数理　物理学的背景からトポロジー, 微分幾何, 関数解析まで.
第1版, サイエンス社, 2015, 1-7.
須藤靖. 解析力学・量子論. 第1版, 東京大学出版会, 2008, 21-41.
京都大学基礎物理学研究所　九後汰一郎ゲージ理論をめぐって — Yang-Mills 50 年 —
http://www2.yukawa.kyoto-u.ac.jp/~qft.web/2004/proc_pdf/kugo.pdf