円の方程式の一般化

円の方程式は高校数学でも習う馴染み深いものだが、少し一般化するだけで様々な曲線が表現可能であることを見て行く。

Lamé曲線
スーバー楕円（Superellipse）
スーパー楕円の一般化
さらなる一般化（Superformula）
参考

Lamé曲線

　
　丸と四角は似ても似つかない形でむしろ対極にあるというイメージすらある。しかし、ここでの内容を知っているとイメージが変わると思う。実際それらの違いは、一つの方程式のパラメータの違いでしかないといえるからだ。
　円の方程式　
$$x^2+y^2 = 1\tag{1}$$
の一般化を考えてみよう。円の方程式の指数2を任意の実数まで拡張したらどうなるだろうか。(2)式はLamé曲線と呼ばれるものだ。
$$|x|^n+|y|^n = 1\tag{2}$$
絶対値をとっているのは普通の円のように閉じた図形に制限するためだ。パラメータnを変化させたときにどのように曲線が変化するか見てみよう。下に(2)式をプロットしたのでスライダーを動かしてパラメータを変化させてみてほしい。すると下記のような挙動をすることが確認できると思う。

n=2のときは(1)式と同じく通常の円を描く。
nを小さくしてゆくと、図形が内側へ収縮してゆく、逆にnを大きくしてゆくと図形が外側へ膨張してゆく。
n=1で円に内接する正方形になる。
n<1では凹な図形となる。特にn=2/3ではアステロイドとなる。
n→0では、座標軸に漸近してゆく。
2<n<∞では、円と正方形の中間的な図形となる。
n→∞では、円に外接する正方形に漸近してゆく。

スーバー楕円（Superellipse）

　さらに(2)式を拡張していこう。円は楕円の縦横比が等しい特別の場合と見なせるから、楕円は円を内包した概念だといえる。この考えにそって(2)式を拡張すると次式が得られる。
$$\left|\frac{x}{a}\right|^n+\left|\frac{y}{b}\right|^n = 1\tag{3}$$
以下にプロットしたのでパラメータを弄ってみてほしい。(2)式に準ずる挙動をすることが確認できると思う。これにより楕円と長方形の中間的な図形が表現可能となる。

　このスーパー楕円は建築やデザインの世界で使われている。実際調べてみるとスーパー楕円の形状をしたテーブルなどが売っているようだ。初めてスーパー楕円が建築に導入されたのはスウェーデン・ストックホルムのセルゲル広場らしい。これはデンマーク人の数学者、デザイナー、哲学者、詩人であるPiet Hein（ピート・ハイン）がデザインしたものだ。ちなみにセルゲル広場のスーパー楕円のパラメータは、a/b=6/5, n=5/2らしい。

セルゲル広場（Wikipediaより引用）

スーパー楕円の面積$A$は次式で与えられる。

\begin{eqnarray}
A=4b\int_0^a \left[ 1-\left(\frac{x}{a}\right)^n \right]^\frac{1}{n} dx\\
=\frac{4^{1-1/n} \ a b \sqrt{\pi} \ \Gamma\left(1+\frac{1}{n}\right)}{\Gamma\left(\frac{1}{2}+\frac{1}{n}\right)}
\end{eqnarray}
n=2やn=∞の場合を確認すると、確かに楕円や長方形の場合も成立していることがわかる。$\Gamma$はガンマ関数で$\Gamma \left( 1/2 \right) = \sqrt{\pi} $、$\Gamma \left( 3/2 \right) = \sqrt{\pi}/2 $である。

スーパー楕円の一般化

　また違う方向の一般化として、xの項とyの項の指数を独立に変化させることが考えられる。すなわち(5)式のような一般も考えられる。n, mを変化させることでx方向とy方向を別々に収縮・膨張させることができることが確認できる。
$$\left|\frac{x}{a}\right|^n+\left|\frac{y}{b}\right|^m = 1\tag{5}$$

さらなる一般化（Superformula）

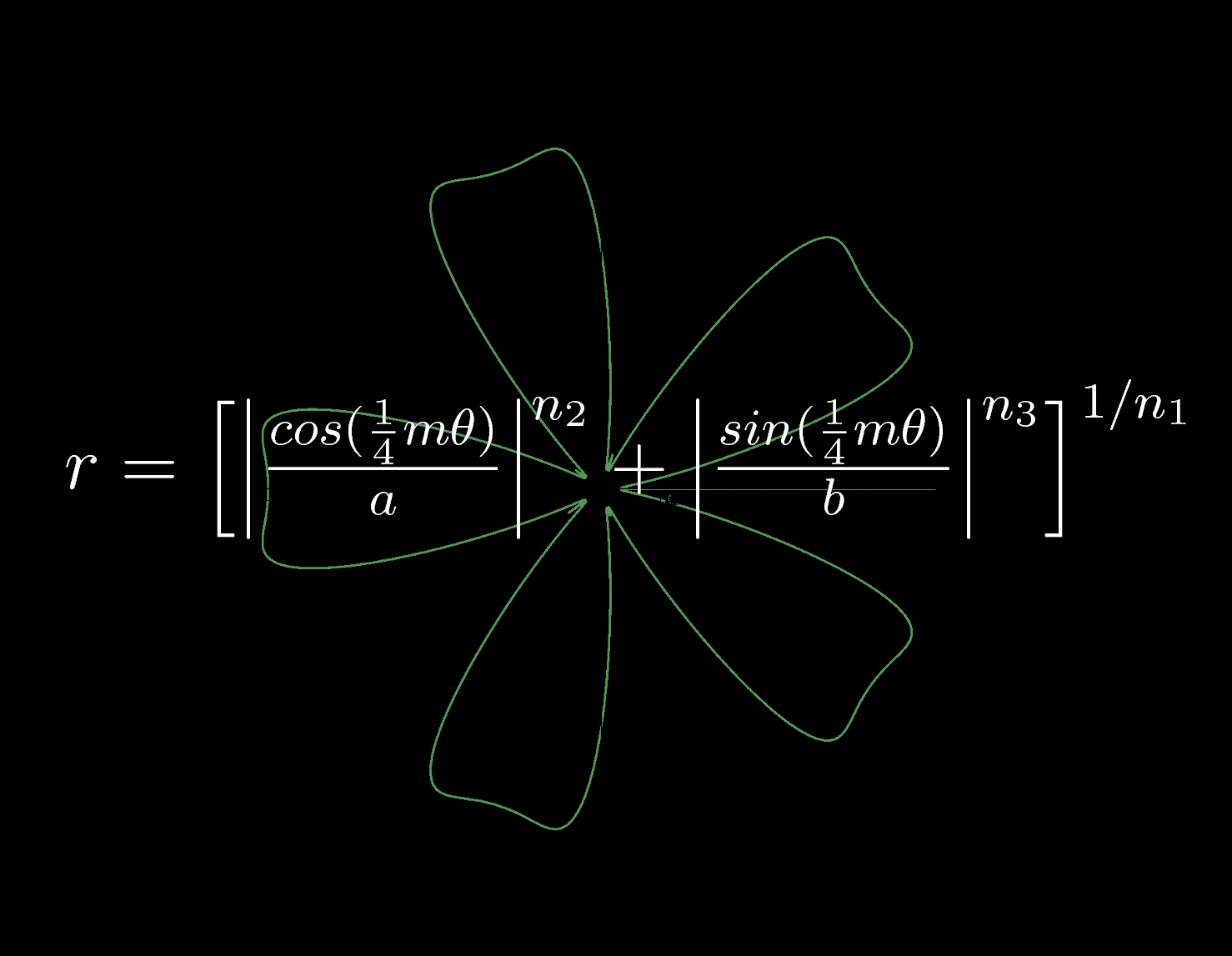
　ベルギーの生物学者のJohan Gielisが発見し”Superformula”と名付けた数式はスーパー楕円のさらなる一般化とみなせるものだ。この一つの方程式で驚くほど多様な形を表現することができる。まあ、パラメータが6つもあるので多様な形を表現できるというのは当然といえば当然なのかもしれないが、それでもこの比較的単純な式から様々な形が生成させるのは興味深い。特に、円の方程式の一般化という全く生物学と無関係なところから出発したのにも関わらず、自然界にある様々な形状を再現できることは面白い。

$$r=\left[\left| \frac{cos(\frac{1}{4}m\theta)}{a} \right|^{n_2}+\left| \frac{sin(\frac{1}{4}m\theta)}{b} \right|^{n_3}\right]^{1/{n_1}}\tag{6}$$

花の形状の例（Wikipediaより引用）