中和滴定曲線をPythonでシミュレーションする

　みなさんは中和滴定という分析化学の手法をご存じだろうか。化学系の大学へ進学した人なら基礎的な実験操作として必ず学生実験で行うと思う。化学を専攻している人でなくても高校の授業や大学の教養課程でやったことがあるひとは多いのではないだろうか。この記事では中和滴定で得られる中和滴定曲線のシミュレーションをPythonを用いて行ったのでその結果を紹介する。

中和滴定について簡単な説明
中和滴定曲線を数学的に厳密に扱いたい
理論式の導出
Pythonでシミュレーションする
まとめ
参考

中和滴定について簡単な説明

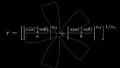
　中和滴定というのは、溶液中に含まれる酸や塩基を定量するための実験手法だ。例えば、酸を定量するためには、濃度が既知の塩基の溶液をビュレットという器具を用いて滴下してゆく。予め酸溶液には指示薬（例えば、フェノールフタレイン等）が添加してあって、塩基を滴下して中和が完了したことを指示薬の呈色反応によって知ることができる。塩基溶液の滴下量に対してpHをプロットすると中和滴定曲線というものが得られる（図１）。等量点の付近ではpHが急激に変化する様子が観察される（pHジャンプ）。

図１　中和滴定曲線（Wikipediaより引用）

中和滴定曲線を数学的に厳密に扱いたい

　中和滴定というのはだいたい上記のようなものなのだが、ある時私はふと思ったことがある。分析化学のテキストをパラパラとめくりながら眺めていて思ったのだが、中和滴定曲線って数学的にはどんな関数なんだっけ？と思ってしまったのである。だいたいテキストには、①当量点に至るまで、②等量点付近、③等量点移行の３つの領域に分けて水素イオン濃度を（即ちpH）を知るための「近似式」が載っているだけだ。理屈が好きな私としては近似無しの理論式が知りたい。そうでないと分かった気にならなくて気持ちが悪い。
　もちろん近似式しか与えられていないのは訳があって、近似無しでまともに水素イオン濃度を与える式を扱おうとすると、３次方程式が出てきたりして手計算するには複雑すぎるのだ。複雑で定性的な理解にも向かないから大抵のテキストには近似式だけ載っているというわけだ。しかし今の時代、プログラマーでなくても家庭用のPCで簡単にプログラミングができる時代なのだから３次方程式くらいPCに力業で解いてもらって結果をプロットしてもらうことだってできる。小学校でもプログラミングをやるらしいし、私のコードをネット上に残しておくことで誰かの助けになれば嬉しいものだ。

理論式の導出

　シミュレーションをするにあたり理論式の導出を行う。以下では酸を塩基で滴定する場合を扱うが、逆に塩基を酸で滴定する場合も取り扱いはおなじなので、酸を塩基で滴定する場合だけを扱う。なお、滴定に用いる塩基は強塩基であることを仮定する。酸溶液中では以下の化学平衡が存在する。HAは一価の酸を表している。

\begin{align} \rm HA\rightleftharpoons H^{+}+A^{-} \tag{1} \end{align}

\begin{align} \rm H_2 O\rightleftharpoons H^{+}+OH^{-} \tag{2} \end{align}

この系に関して(3)～(6)式が成立する。\(C_{A}\)は酸の全濃度を表す。

\begin{align} K_w=\rm \left[ H^{+}\right] \left[ OH^{-}\right] \qquad (水のイオン積)\tag{3} \end{align}

\begin{align} K_a=\rm \dfrac {\left[ H^{+}\right] \left[ A^{-}\right] }{\left[ AH\right] } \qquad (酸解離定数)\tag{4} \end{align}

\begin{align}
\ \ C_A=\rm \left[ A^{-}\right] +\left[ AH\right] \qquad (酸の物質収支の式) \tag{5} \end{align}

\begin{align}
\ \ \ C_B=\rm \left[ B^{+}\right] +\left[ BOH\right] \qquad (塩基の物質収支の式) \tag{6} \end{align}

\begin{align} \rm \left[ H^{+}\right] +\left[ B^{+}\right] =\left[ OH^{-}\right] +\left[ A^{-}\right] \qquad (電気的中性の式)\tag{7} \end{align}

(3)式より

\begin{align} {\rm \left[ OH^{-}\right] } =\dfrac {K_{w}}{\rm{ \left[ H^{+}\right] } } \tag{8} \end{align}

(4), (5)式より

\begin{align} {\rm \left[ A^{-}\right] } =\dfrac {K_{a}C_{A}}{K_{a}+ {\rm \left[ H^{+}\right] } } \tag{9} \end{align}

塩基は強塩基と仮定しているので(6)式は

\begin{align} C_B=\rm \left[ B^{+}\right] \tag{10} \end{align}

としてよい。(8), (9), (10)式を(7)式へ代入して整理すると

\begin{align}
{\rm \left[ H^{+}\right] ^{3}}+\left( K_a+C_{B} \right) {\rm \left[ H^{+}\right] ^{2} }+ \left( C_{B} K_{a}-K_{a}C_{A}-K_{w}\right) {\rm \left[ H^{+}\right] } -K_{w}K_{a}=0
\tag{11}
\end{align}

と\(\rm \left[ H^{+}\right]\)についての３次方程式を得る。ここで\(C_{A},C_{B}\)は、滴下による体積変化によっても変化する。滴下前の初期濃度を\(C_{A0},C_{B0}\)とし、酸溶液の体積を\(V_A\)、滴下した塩基溶液の体積を\(V_B\)とすると、体積変化による濃度変化は(12), (13)式で表される。

\begin{align} C_A=C_{A0}\frac{V_A}{V_A+V_B} \tag{12} \end{align}

\begin{align} C_B=C_{B0}\frac{V_A}{V_A+V_B} \tag{13} \end{align}

\(K_w, K_a, C_{B0}, V_{A}\)は実験的に既知だが、\(C_{A0}\)については未知なのでシミュレーションを行うに当たり決めてやる必要がある。（実験ではこの\(C_{A0}\)こそが求めたい量になる。）
　この条件の下、(11)式を\(\rm \left[ H^{+}\right]\)について解き、(12), (13)式を考慮すると\(\rm \left[ H^{+}\right]\)が\(V_B\)の関数として得られて、対数とればこれが中和滴定曲線である。

強酸のときは\(K_{a}\rightarrow \infty\)の極限と見なせるから、(11)の両辺を\(K_a\)で除して極限操作を行うことで

\begin{align}
\left[ H^{+}\right] ^{2}+\left( C_{B}-C_{A}\right) \left[ H^{+}\right] -K_w=0
\end{align}

を得る。この２次方程式を解くことで強酸を強塩基で滴定した場合のpH変化を知ることができる。

Pythonでシミュレーションする

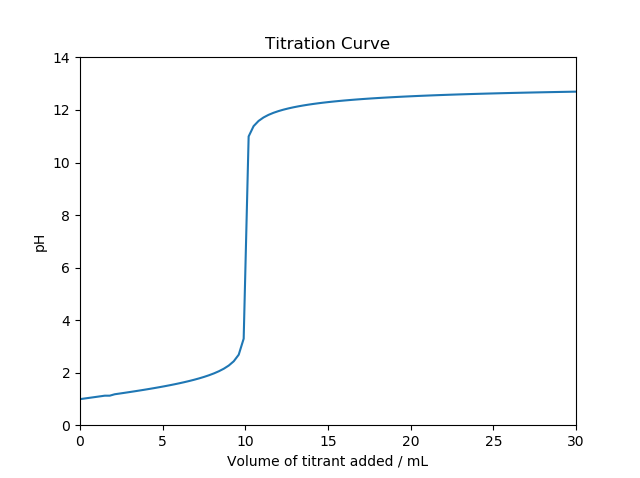
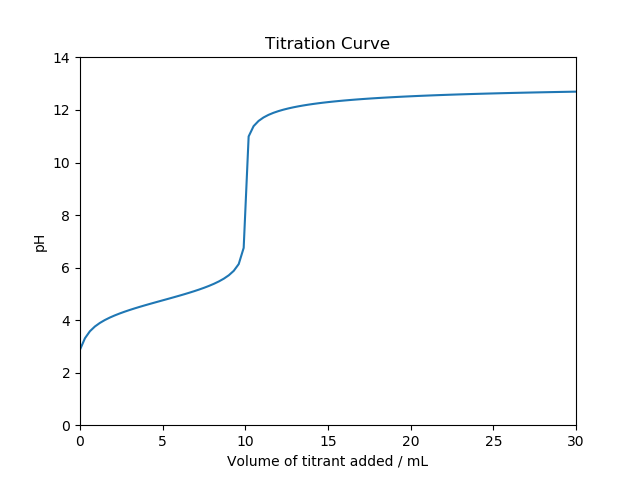
　シミュレーションのコードを以下に示す。シミュレーションは、塩酸（\(K_a=1\times 10^{8}\)；図１）と酢酸（\(K_a=1.75\times 10^{-5}\)；図2）の２種類について行った。

import matplotlib.pyplot as plt
from sympy import Symbol, solve, re, im
import math

x = Symbol('x')
Ka = Symbol('Ka')
Kw = Symbol('Kw')
CA = Symbol('CA')
B = Symbol('B')

Ka = 1.75 * 10**(-5)   #酸のKaを設定
Kw = 1.008 * 10**(-14) #水のイオン積

plot_num = 100  #プロットする点の数
VB_max = 30     #横軸を30mLまで計算
VB_step = VB_max/plot_num  #計算ステップ幅
VB_val = []  #横軸の値を入れる空リスト
pH_val=[]    #縦軸の値を入れる空リスト

#横軸の値を追加
for num in range(plot_num+1):
    VB_val.append(num*VB_step)

for VB in VB_val:
    CA = 1 / (VB+10)       #滴下による希釈の効果（酸）
    B = 0.1 * VB / (VB+10) #滴下による希釈の効果（塩基）

    #３次方程式を解く
    expr =x**3+(Ka+B)*x**2+(Ka*B-Ka*CA-Kw)*x-Ka*Kw
    t_expr = solve(expr, x)

    #正の実数解を取り出す
    for n in range(3):
        if  im(t_expr[n]) < 10**(-20):
            t_expr[n] = re(t_expr[n])
            if t_expr[n] > 0:
                pos_x = t_expr[n]

    #正の実数解をリストに追加
    pH_val.append(-math.log10(pos_x))

#グラフを描画
plt.title('Titration Curve')
plt.xlabel('Volume of titrant added / mL')
plt.ylabel('pH')
plt.xlim(0,30)
plt.ylim(0,14)
plt.plot(VB_val, pH_val)
plt.show()

　図１の引用元に掲載されている中和滴定曲線を再現することができた。強酸を滴定した場合よりも弱酸を滴定した場合のほうが等量点付近でのpH変化が小さいことも再現できている。酢酸よりもさらに弱い酸の場合でシミュレーションを行えば、当量点が段々と不明瞭になって行くことも確かめることができるはずだ。